
Mathematics Specialist is one of the most challenging courses offered by the School Curriculum and Standards Authority (SCSA) in Western Australia. It's designed to prepare high-achieving students for advanced studies in mathematics, engineering, and sciences.
In this comprehensive article, we'll cover everything from syllabus breakdown to exam strategies, helping you boost your confidence and performance. Whether you're aiming for that top A grade or looking to improve your current standing, you'll find valuable insights to elevate your Maths Specialist game.
Let's dive in and unlock your potential for the WACE Mathematics Specialist exam!
Summary of Units
Below we will cover Units 3 and 4 in Year 12 -Mathematics Specialist and all the sub-topics you will need to understand to do well on your Mathematics Specialist exam:
Unit 3
This unit covers three main topics: Complex numbers, Functions and graph sketching, and Vectors in three dimensions. Students build on prior knowledge of two-dimensional vectors and explore three-dimensional vectors, vector equations, and vector calculus, integrating concepts from the Mathematics Methods ATAR course.
The unit also extends the study of complex numbers to the polar form, while advancing skills in functions and graph sketching to solve integration problems. Technology is required for computational aspects throughout the course.
Topic 3.1: Complex numbers (18 hours)
Cartesian forms
3.1.1 review real and imaginary parts Re(z) and Im(z) of a complex number z
3.1.2 review Cartesian form
3.1.3 review complex arithmetic using Cartesian forms
Complex arithmetic using polar form
3.1.4 use the modulus |z| of a complex number z and the argument Arg (z) of a non-zero complex number z and prove basic identities involving modulus and argument
3.1.5 convert between Cartesian and polar form
3.1.6 define and use multiplication, division, and powers of complex numbers in polar form and thegeometric interpretation of these
3.1.7 prove and use De Moivre’s theorem for integral powers
The complex plane (The Argand plane)
3.1.8 examine and use addition of complex numbers as vector addition in the complex plane
3.1.9 examine and use multiplication as a linear transformation in the complex plane
3.1.10 identify subsets of the complex plane determined by relations such as
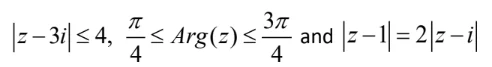
Roots of complex numbers
3.1.11 determine and examine the nth roots of unity and their location on the unit circle
3.1.12 determine and examine the nth roots of complex numbers and their location in the complex plane
Factorisation of polynomials
3.1.13 prove and apply the factor theorem and the remainder theorem for polynomials
3.1.14 consider conjugate roots for polynomials with real coefficients
3.1.15 solve simple polynomial equations
Topic 3.2: Functions and sketching graphs (16 hours)
Functions
3.2.1 determine when the composition of two functions is defined
3.2.2 determine the composition of two functions
3.2.3 determine if a function is one-to-one
3.2.4 find the inverse function of a one-to-one function
3.2.5 examine the reflection property of the graphs of a function and its inverse
Sketching graphs
3.2.6 use and apply x for the absolute value of the real number x and the graph of y = |x|3.2.7 examine the relationship between the graph of
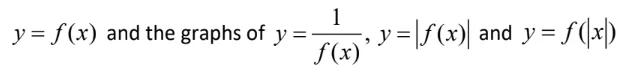
3.2.8 sketch the graphs of simple rational functions where the numerator and denominator are polynomials of low degree
Topic 3.3: Vectors in three dimensions (21 hours)
The algebra of vectors in three dimensions
3.3.1 define the concept of a vector in three dimensions, using the unit vectors i, j and k, determining magnitude, scalar (dot) product and parallel and perpendicular vectors
3.3.2 prove geometric results in the plane and construct simple proofs in 3 dimensions
Vector and Cartesian equations
3.3.3 introduce Cartesian coordinates for three dimensional space, including plotting points and equations of spheres
3.3.4 use vector equations of curves in two or three dimensions involving a parameter and determine a corresponding’ Cartesian equation in the two-dimensional case
3.3.5 determine a vector equation of a straight line and straight line segment, given the position of two points or equivalent information, in both two and three dimensions
3.3.6 examine the position of two particles, each described as a vector function of time, and determine if their paths cross or if the particles meet
3.3.7 use the cross product to determine a vector normal to a given plane
3.3.8 determine vector and Cartesian equations of a plane
Systems of linear equations
3.3.9 recognise the general form of a system of linear equations in several variables, and use elementary techniques of elimination to solve a system of linear equations
3.3.10 examine the three cases for solutions of systems of equations – a unique solution, no solution, and infinitely many solutions – and the geometric interpretation of a solution of a system of equations with three variables
Vector calculus
3.3.11 consider position vectors as a function of time
3.3.12 derive the Cartesian equation of a path given as a vector equation in two dimensions, including ellipses and hyperbolas
3.3.13 differentiate and integrate a vector function with respect to time
3.3.14 determine equations of motion of a particle travelling in a straight line with both constant and variable acceleration
3.3.15 apply vector calculus to motion in a plane, including projectile and circular motion

Unit 4
This unit covers three topics: Integration and its applications, Rates of change and differential equations, and Statistical inference. Students continue their study of differentiation and integration, applying these techniques to solve simple differential equations, especially in biology and kinematics.
Real-world applications of mathematics are emphasised throughout. The unit also consolidates students' knowledge of probability and statistics, focusing on statistical inference for sample means and confidence intervals. Technology is required for computational aspects.
Topic 4.1: Integration and applications of integration (20 hours)
Integration techniques

Applications of integral calculus

Topic 4.2: Rates of change and differential equations (20 hours)
Applications of differentiation

Modelling motion

Topic 4.3: Statistical inference (15 hours)
Sample means

Confidence intervals for means

💡Study tip! Organise your notes by the headers and sub-headers in the syllabus. This ensures you cover everything that could be on the exam and keeps your notes super organised.
WACE Mathematics Specialist Exam Format
Content Area Weightings (across both sections)
Note: A formula sheet is provided. For questions worth more than two marks, valid working or justification is required for full marks.
💡Take notes efficiently and effectively using these tips!
What Does an A Look Like?
Are you curious as to what it takes to get an A? In the syllabus, the Department of Education in Western Australia outlines exactly what is required for a student to get an A in Mathematics Specialist.
Revision Tips and Mistakes to Avoid
How to Revise
- Master Calculator-Free Techniques:
- Practise algebraic manipulations without relying on a calculator
- Focus on mental math and estimation skills for Section One
- Optimise Calculator Use:
- For Section Two, become proficient with your CAS calculator
- Learn shortcuts and efficient methods for complex calculations
- Strengthen Conceptual Understanding:
- Focus on understanding the 'why' behind formulas and methods
- Create concept maps linking different topics (e.g., how calculus relates to vectors)
- Practise Proofs and Mathematical Communication:
- Improve your ability to construct and write mathematical proofs
- Practice explaining your reasoning clearly, as required for full marks
- Utilise Past Papers Strategically:
- Complete timed practice using official WACE past papers
- Analyse the marking guidelines to understand how marks are allocated
- Develop Exam Technique:
- Practise identifying the most efficient method to solve each question type
- Learn to extract relevant information from complex word problems
- Review Formula Sheet:
- Familiarise yourself with the provided formula sheet
- Practice applying these formulas to various problem types
- Simulate Exam Conditions:
- Practise with the same time constraints and resources you'll have in the actual exam
- Get comfortable with the transition between calculator-free and calculator-assumed sections
💡Check out these scientifically proven strategies to improve how you study!

Mistakes to Avoid
- Neglecting Calculator-Free Skills
- Don't over-rely on your calculator for basic operations
- Practice algebraic manipulations and mental math for Section One (50 minutes, 35% of exam)
- Mismanaging Time Between Sections
- Avoid spending too much time on Section One at the expense of Section Two
- Remember: Section Two (Calculator-assumed) is 100 minutes and worth 65% of the exam
- Ignoring the Provided Formula Sheet
- Don't waste time memorising formulas that are provided
- Practice applying these formulas efficiently in various contexts
- Misreading Question Requirements
- Pay attention to whether a question asks for exact answers or decimal approximations
- Note when a question requires proof or just calculation
- Overlooking Units and Context
- Don't forget to include units in your final answers
- Ensure your answers make sense in the context of Western Australian-specific word problems
- Neglecting to Show Working
- Remember, for questions worth more than two marks, you need to show valid working for full marks
- Clear, logical steps are crucial, especially in the vectors and calculus sections
- Focusing Too Narrowly on Specific Topics
- Don't neglect any content areas; all have significant weightings:
- Complex numbers (15-20%)
- Functions and graphs (10-15%)
- Vectors in three dimensions (15-20%)
- Integration and applications (15-20%)
- Rates of change and differential equations (15-20%)
- Statistical inference (10-15%)
- Don't neglect any content areas; all have significant weightings:
- Misusing the CAS Calculator
- In Section Two, avoid using the calculator for simple calculations that can be done mentally
- Don't rely solely on the calculator without understanding the underlying concepts
💡Remember, success in the WACE Mathematics Specialist exam comes from a balanced approach to all topics, strong fundamental skills, and the ability to apply knowledge in various contexts. Avoiding these common mistakes will help you maximise your performance on exam day.
Link to Past Papers
Why Past Papers are the Best Way to Revise
- Familiarisation with WACE Question Structure
- WACE exams tend to use consistent question structures, which may differ from textbooks or other resources
- Regular practice with past papers helps you become comfortable with these specific structures
- This familiarity can save time and reduce stress during the actual exam
- Identifying Personal Strengths and Weaknesses
- Quickly pinpoint which types of questions and content areas you find challenging
- Focus your revision efforts on areas that need improvement
- For example, you might discover you need more practice with complex number proofs or vector calculus applications
- Time Management Practice
- Identify parts of the exam where you need to allocate more time
- Practise balancing time between the calculator-free (50 minutes, 35% of exam) and calculator-assumed (100 minutes, 65% of exam) sections
- Learn to pace yourself for longer, multi-part questions often found in the calculus and vectors sections
- Understanding Mark Allocation
- Past papers show how marks are typically distributed across different question types
- Learn which steps are crucial for earning full marks, especially in proof-based questions
- Understand the level of working required for questions worth more than two marks
- Familiarity with Exam Layout and Instructions
- Become accustomed to the format of having separate calculator-free and calculator-assumed sections
- Practise using the formula sheet provided in past exams
- Understand common instructions and terminology used in WACE exams
- Developing Effective CAS Calculator Strategies
- Past papers help you refine your use of CAS calculators for Section Two
- Learn which types of questions benefit most from calculator use and which are better solved manually
- Improving Answer Presentation Skills
- Learn how to structure your responses clearly and logically
- Understand the level of explanation expected, especially in proof-based questions
- Identifying Common Themes and Recurring Concepts
- Recognise patterns in how certain topics (e.g., complex numbers, vectors, calculus) are examined year after year
- Anticipate potential question types and prepare accordingly
❗Caution Note:When reviewing exams from several years ago, be aware that some topics may no longer be part of the current syllabus or may be examined differently. Always cross-reference with the most recent syllabus document and more recent past papers. For example, the weighting of topics or the balance between calculator-free and calculator-assumed sections may have changed over time.
By consistently working through WACE Mathematics Specialist past papers, you'll not only reinforce your understanding of the content but also develop the specific skills and strategies needed to excel in this challenging exam.

Final Preparation Tips for WACE Mathematics Specialist Exam
Week Before the Exam
- Review Key Concepts:
- Focus on high-weighted areas: complex numbers, vectors, calculus, and differential equations
- Create summary sheets for each major topic
- Practise Calculator Skills:
- Ensure you're proficient with your CAS calculator for Section Two
- Practice efficient use for complex calculations and graphing
- Timed Practice:
- Complete at least one full past paper under timed conditions
- Practise transitioning between calculator-free (50 minutes) and calculator-assumed (100 minutes) sections
- Revise Proof Techniques:
- Review common proof methods used in complex numbers and vector questions
- Practice explaining your reasoning clearly in writing
- Formula Sheet Familiarity:
- Memorise the location of formulas on the provided sheet
- Practice quickly applying these formulas to various question types
- Mental Math Refresher:
- Sharpen your mental math skills for the calculator-free section
- Practice basic integration and differentiation without a calculator
- Review Mark Schemes:
- Understand how marks are typically allocated in WACE Math Specialist exams
- Focus on commonly tested concepts and question styles
Night Before the Exam
- Light Review:
- Briefly go over your summary sheets
- Focus on areas you find challenging, like statistical inference or vector calculus
- Organise Materials:
- Pack your CAS calculator (with fresh batteries) and spares
- Prepare several pens, pencils, and erasers
- Check Exam Details:
- Confirm the exam time and location
- Plan your travel to arrive at least 30 minutes early
- Relaxation:
- Do some light exercise or meditation to reduce stress
- Avoid heavy studying; trust in your preparation
- Early Bedtime:
- Aim for at least 8 hours of sleep to ensure mental alertness
.webp)
Day of the Exam
- Healthy Breakfast:
- Eat a nutritious, balanced meal to maintain energy levels
- Arrival:
- Get to the exam venue early
- Use any waiting time for light revision or calming techniques
- Last-Minute Review:
- Quickly scan your formula sheet to refresh your memory
- Do a few simple calculations to warm up your math brain
- Exam Strategy:
- Read all instructions carefully
- In Section One (calculator-free), focus on showing clear working
- In Section Two, efficiently use your CAS calculator for complex problems
- Time Management:
- Allocate time based on mark values (roughly 1 minute per mark)
- Leave time to check your answers, especially for high-value questions
- Tackling Difficult Questions:
- If stuck, especially on vector or complex number problems, try sketching or breaking the problem into smaller parts
- For integration questions, consider different techniques (substitution, partial fractions) if one method doesn't work
- Stay Calm:
- If you encounter a challenging question, take a deep breath and move on
- Remember, you can always come back to it if time allows
- Final Check:
- In the last few minutes, ensure you've answered all questions
- For calculation-heavy questions (like in calculus or statistical inference), quickly verify your results make sense
💡Remember, the WACE Mathematics Specialist exam tests not just your knowledge, but your ability to apply it under pressure. Stay confident in your preparation and approach each question methodically.
Conclusion
Success in the WACE Mathematics Specialist exam stems from thorough understanding, consistent practice with past papers, and strategic preparation. In the final week, focus on consolidating your knowledge and maintaining your well-being. On exam day, stay calm, manage your time wisely, and approach each question methodically.
If you need additional support, consider seeking a tutor experienced with the WACE Mathematics Specialist curriculum.
Trust in your preparation and showcase your mathematical skills with confidence. You're well-equipped to excel – good luck!








